Shift-Reduce Parsing with a Graph-Structured Stack
December 2, 2011
During my Honours thesis, I was performing natural language parsing (NLP). NLP aims to allow computers to efficiently analyze, understand and even generate natural language.
My focus was on parsing language, or determining the structure of a sentence. This is similar to parsing programming languages, something you're more likely familiar with, except that natural language is ambiguous. The phrase "I saw the girl on the hill with the telescope" has many possible different derivations, for example. A few example interpretations: the girl may be on the hill, the girl may be on the hill which has a telescope, the girl may have set up her telescope on the hill or you may have seen her with a telescope.
This ambiguity makes parsing a difficult task as there may be millions of different possible derivations. Whilst there are ways to do this efficiently (with the CKY algorithm being one of the most popular), I had to perform the parsing incrementally. This led me to use shift-reduce (SR) parsing. SR parsing is quite popular amongst programming language parsing as it's quite efficient for unambiguous languages. For ambiguous languages, however, parsing takes worst-case exponential time. With the addition of a relatively unexplored data structure, the Graph-Structured Stack (GSS), this can be reduced down to worst-case polynomial time.
Shift-Reduce Parsing
stack = [] # Start with the empty stack -- ∅ stack.append("A") # Shift stack.append("B") # Shift stack.append("C") # Shift stack.append("D") # Shift stack.append("E") # Shift # stack = ["A", "B", "C", "D", "E"]
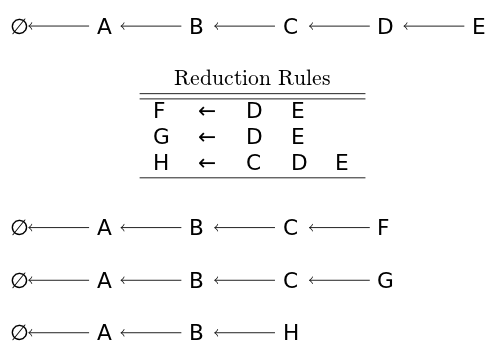
Deterministic Recogniser SR Parser
from collections import deque sent = deque(list("ABCDEI")) stack = [] rules = [ (("D", "E"), "F"), (("D", "E"), "G"), (("C", "D", "E"), "H"), (("F", "I"), "J"), (("G", "I"), "J") ] prev_stack = None while sent or prev_stack != stack: # Print out the stack and store it for later comparison print "Stack:", stack prev_stack = stack[:] # Try all reduction rules for rule, result in rules: if tuple(stack[-len(rule):]) == rule: print "+ Reduce with %r => %r" % (rule, result) [stack.pop() for x in rule] stack.append(result) continue # If there are tokens left in the input, shift if sent: stack.append(sent.popleft()) print "+ Shift on %s" % stack[-1]
The Graph-Structured Stack
The graph-structured stack is based around three key concepts:
- Splitting
- Combining
- Local Ambiguity Packing
Splitting
The graph-structured stack makes the reduce operation non-destructive by creating a new head for each possible derivation. Below we can see there are now four heads to the graph structured stack.
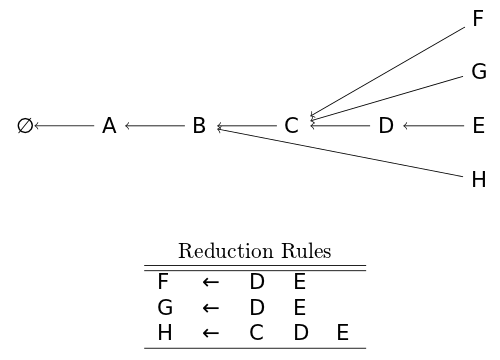
Combining
When a new node is shifted, it is combined with each of the heads of the graph-structured stack. This means that only a single shift operation is needed instead of n shift operations where n is the number of possible derivations in the previous step.
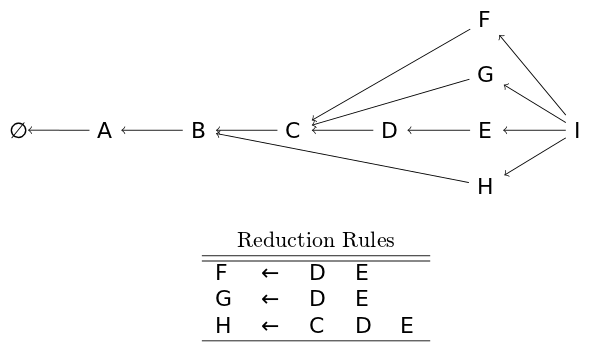
Local Ambiguity Packing
Finally, if two reduction rules produce the same node (for whatever we define "same" as), the two nodes are merged into a single node. In the case below, two rules produce an equivalent node J (their stacks are equivalent as can be seen by the back pointer), so they are merged into a single J node.
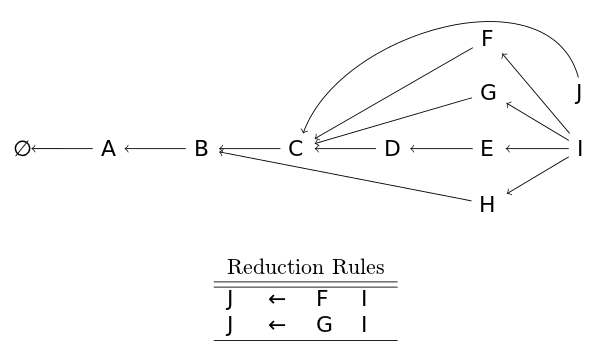
Popular Articles
- It's ML, not magic: machine learning can be prejudiced
- It's ML, not magic: the rise of AI-prefix investing
- In deep learning, architecture engineering is the new feature engineering
- How Google Sparsehash achieves two bits of overhead per entry using sparsetable
- Where did all the HTTP referrers go?
Interested in saying hi? ^_^
Follow @Smerity