How Google Sparsehash achieves two bits of overhead per entry using sparsetable

May 25, 2015

Google Sparsehash was released in 2005 and offered two different hash table implementations - Densehash for speed and Sparsehash for space. The Sparsehash implementation remains one of the most space efficient hash tables available, requiring only two bits of overhead per entry. Given that just saying whether something exists or not costs a bit, that's not too bad. It's even performant - only two to three times slower than most other C++ hash table libraries.

How is it possible to be that space efficient whilst still maintaining reasonable performance? Today I'll be explaining, in relatively plain English, how the sparse array underlying Google Sparsehash, called sparsetable, works.

Hash Table and Open Addressing Review

If you are comfortable with how hash tables work, specifically if the phrase "open addressing using linear / quadratic probing" doesn't make you question your sanity, feel free to skip this section.

Hash tables are one of the magical data structures of computer science. In the early days of computing, an 8-bit deity came down in all his/her pixelated goodness and delivered unto us a data structure that allows for O(1) insertion, deletion, and lookup. It's even easy to implement.

Hash tables store key-value pairs, such as going from an email to a name, where the email would be the key and the name the value.

Email => Name smerity@smerity.com => Stephen Merity

Hash tables are also frequently referred to as dictionaries, specifically as that's exactly what they become if we set the key to be a word and the value to be the word's description.

For a full description of hash tables and how they achieve such quick insertion and lookup times, there are likely far better sources available than I could produce.

To fully grok the contents below, you simply need to know that:

• Underlying a hash table is a large array of length N. Most of these slots are empty. Empty slots are bad as you're wasting a large amount of space.
• If we use chaining for handling collision, each slot in the array is a linked list. This results in a large amount of overhead as each element in the linked list must store a 32 or 64 bit pointer.
• If we use open addressing for handling collision, we must be very wary with how many empty slots are in the array. If too many slots are taken, lookup can devolve (in the worst case) to an O(n) traversal. This means we need to keep the load factor low as otherwise we'll hurt performance, but keeping the load factor low means we're wasting space.

Introducing sparsetable

The underlying reason why hash tables are space inefficient is that we need to store a very large array in order to ensure we have good performance. How large? If we are using open addressing, one would generally leave 20-50% of the space empty. If we allow the empty space to drop too low, the hash table can degenerate into a full traversal to find items - O(N). Given hash tables are usually featured in the inner loop of more complex algorithms, the not too bad sounding O(N) rapidly becomes a "why is my computer on fire!?!?" problem.

As such, the easiest way to minimize the size of the hash table is by minimizing the size of the array. Whilst we only discuss sparse tables, there are many more interesting data structures that use space close to the information theoretic minimum under the field of succinct data structures.

Understanding Sparsetable

Traditional arrays of size N require N x len(obj) bytes, even if only one slot in the array is used. In the image below, an array of length 16 only stores 6 elements, wasting 10 of the slots.

Sparsetable solves this issue by creating an array where elements that are "empty" only require a small amount of storage compared to the size of the element it would contain if it were full. Sparsetable is able to get this all the way down to 1 bit of storage for each unused element whilst still allowing constant time insertion, deletion, and lookup.

We can represent the image above by breaking the array into small buckets - in this case, a bucket covers four elements. Each bucket needs to know which elements are stored and have a space for storing those elements. To know which elements are stored, we can turn to a binary string, such as 0100 for the first bucket.

For the full example above, the binary string becomes 0100|1001|0000|1011. This costs 1 bit per element, regardless of whether the slot is empty or full.

For real tasks however we also want to store objects in each of these array slots. To do this, we then create a real array for each bucket, exactly the length required to store the active elements - i.e. the number of 1's in the bucket's binary string. This wastes no space at all, as the array stores exactly what we need it to store.

When we want to retrieve an item from a given slot, we work out which bucket it's in and count how many used slots are before it. For example, if we wanted to get the third element of the bucket 1011 (one-indexed, so the value of __X_), we'd see that there is one item stored before it, meaning the slot is actually in the second position of the array.

Google Sparsehash uses 2 bits per empty item however - so where does that extra bit comes from? We need to store a pointer to the bucket's array. In our toy case this is expensive as our buckets hold very few elements each. A 64 bit pointer for four elements results in 16 bits of overhead per element. If we're lucky and on a 32 bit system, that's only 8 bits of overhead per element. In the case of sparsetables, each bucket holds 32 * x + 16 elements (why that formula?), resulting in far more reasonable overheads for empty slots.

(here's a secret: Sparsehash only uses 2 bits of overhead for empty slots on 32 bit machines - on 64 bit machines the pointer overhead means it's 2.67)

Advantages of SparseHash over traditional hash tables

When the load factor of a Sparsehash hash table grows too large, the underlying sparsetable is able to be doubled with only a minor increase in memory usage - two bits of overhead per empty slot. Even for a billion empty slots, that's only 250 megabytes of overhead. Sparsehash is also able to move items from the smaller Sparsehash to the larger Sparsehash essentially in-place by moving over a single bucket at a time.

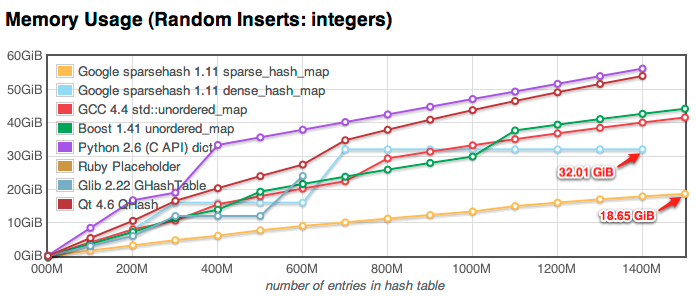
The graph above, from Big Memory, Part 3.5: Google sparsehash! by Neustar Research, shows how smoothly Sparsehash is able to grow. The other hash table libraries all experience blocky growth, caused by increases in the underlying array size to keep the load factor reasonable. For certain applications, being able to accurately predict memory usage is vastly important, and it's in these situations Sparsehash really comes out ahead.

Conclusion

Whilst Sparsehash aims to be memory efficient, it doesn't sacrifice speed to achieve its goal.

Best of all, the theory behind this well crafted implementation lends itself to other arenas. Indeed, Redis accidentally implements something quite similar to this by their use of zipmaps!

For me, the key point is that even if we have machines with 244GB of RAM available at our fingertips, we will always find a new task that leaves us begging for that extra gigabyte. Sparsehash can save us in those cases. The fact we end up only two to three times slower than most other C++ hash table libraries should make us cry for joy.

References

• Big Memory, Part 3.5: Google sparsehash! as part of the fascinating Big Memory series from Neustar
  (for "fun" that involves crying hysterically into a box of tissues, compare hash table performance between C++ and Java in Part 4)
• Hand Coded Assembly Beats Intrinsics in Speed and Simplicity for deep discussion on popcnt, which would be used for counting the number of active slots are in a bucket (i.e. count how many times 1 appears in the bucket's bitstring of 10110100)
• Redis weekly update Number 7 - Full of keys where antirez suggests an approach which closely resembles Sparsehash's (i.e. small hashtables in Redis are implemented as a zipmap - a flat array - mimicking the bucket strategy above)
• Storing hundreds of millions of simple key-value pairs in Redis where the Instagram team implemented a similar solution to antirez by taking advantage of zipmaps